HTE

El objetivo de este módulo es proponer un caso que puedas analizar en tu propio computador.

1. Percepciones sobre el gasto público

Los datos provienen de la base de datos \(welfare\) del artículo de Green & Kern (2012). La Encuesta Social General (GSS, por sus siglas en inglés) es una encuesta comúnmente utilizada en Estados Unidos, la cual presenta efectos experimentales altamente replicados y una muestra suficientemente grande para ser analizada adecuadamente.

La base de datos evalúa las percepciones que tienen los estadounidenses sobre programas de gobierno que se alineen al denominado “Estado de Bienestar” (\(welfare\)), puesto que existe un prejuicio generalizado hacia programas y beneficios sociales. Un experimento conocido sobre esta encuesta asigna aleatoriamente a los respondentes a una evaluación de si el gasto público es “demasiado alto”, “adecuado” o “demasiado bajo”, en determinados programas. La condición experimental varía una única palabra en el fraseo de uno de los programas sociales: el tratamiento consiste en utilizar la palabra “bienestar” en vez de la frase “asistencia a los pobres” (welfare/assistance to the poor).

Los resultados de numerosos análisis de esta encuesta, desde 1986 hasta 2010, muestran que al ser expuestos al fraseo del programa como “bienestar social” (welfare), los encuestados muestran una probabilidad de 30% y 50% más de responder que el gasto es “demasiado alto” (too much). Algunas de las razones expuestas para explicar estas diferencias se basan en estereotipos generalizados sobre los beneficiarios de los programas de bienestar y de la gente más pobre, particularmente en estereotipos raciales; también se esgrimen argumentos sobre orientaciones político-ideológicas sobre individualismo y conservadurismo.

El estudio que se busca replicar en este tutorial estudia la heterogeneidad de dicho tratamiento.

1.1. Datos

La base de datos puedes descargarla en el siguiente enlace.

Green, D. P., & Kern, H. L. (2012). Modeling heterogeneous treatment effects in survey experiments with Bayesian additive regression trees. Public opinion quarterly, 76(3), 491-511.

Este tutorial es una adaptación del tutorial “Estimation of Heterogeneous Treatment Effects” realizado por Athey, Wager, Hadad, Klosin, Muhelbach, Nie y Schaelling en mayo de 2020 para su curso de “Machine Learning and Causal Inference”.

1.2. Cargar las librerías en R

Comience cargando las librerías que usaremos en este tutorial. A ellas debe agregarles las tradicionales usadas para cargar la base de datos y algunas de manejo básico de bases.

library(fBasics)
library(grf)
library(ggplot2)
library(estimatr)
library(dplyr)

1.3. Preparar los datos

Limpiaremos de datos faltantes, y botaremos aquellas columnas que no sean variables de resultado, de tratamiento o covariables.

df <- read_csv("welfarelabel.csv")
df <- na.omit(df)
df <- df %>% select(-c("id", "_merge"))

Puede ser una buena práctica cambiar el nombre de las variables, para utilidad posterior. Como utilizaremos funciones recientes de Causal Trees y Causal Random Forests, propuestas por Athey y otros, estas todavía no aceptan datos categorizados como “factor”, por lo que es recomebdable transformarlos a “numeric”. Para esto último utilizaremos las funciones lapply( ) y as.numeric( ).

df <- df %>% rename(Y=y,W=w)
df <- data.frame(lapply(df, function(x) as.numeric(as.character(x))))

Comenzaremos el análisis echando una mirada al contenido de la base de datos. Para ello, veremos los estadísticos descriptivos de las variables. Para eso, puede utilizar las funciones de la librería fBasics, la cual debe estar instalada para poder usarse.

# Hacemos una matriz con los estadísticos
summ_stats <- fBasics::basicStats(df)
summ_stats <- as.data.frame(t(summ_stats))

# Le ponemos títulos a la matriz para facilitar la lectura
summ_stats <- summ_stats[c("Mean", "Stdev", "Minimum", "1. Quartile", "Median",  "3. Quartile", "Maximum")] %>% 
  rename("Lower quartile" = '1. Quartile', "Upper quartile"= "3. Quartile")

summ_stats

Se dejará un 20% de la muestra para validación, y se utilizará el \(80\%\) de los datos para entrenar los árboles.

train_fraction <- 0.80
n <- dim(df)[1]
train_idx <- sample.int(n, replace=F, size=floor(n*train_fraction))
df_train <- df[train_idx,]
df_test <- df[-train_idx,]

¿Cuál es la proporción de individuos tratados en la muestra?

\[\\[1in]\]

2. Estimando Heterogeneidad

Para estimar el Random Forest utilizamos la función causal_forest del paquete grf. Debemos indicar cuáles son las covariables, la variable de resultado y la variable de tratamiento. Para esto primero definimos tales variables.

cf <- causal_forest(
  X = as.data.frame(df_train %>% select(-c("Y", "W"))),
  Y = df_train$Y,
  W = df_train$W,
  num.trees = 1000
)

De acuerdo a Athey, un buen número de árboles a utilizar es el número de individuos en la muestra. ¡Prueba en tu computador cambiando el número de árboles a estimar!

2.1 Examinando la región de soporte común

Un supuesto importante de la estimación en inferencia causal es que existe una región de soporte común. Esto es, que hay observaciones tratadas y no tratadas en la misma región. Para eso, estudiaremos el Propensity Score estimado por la función.

La predicción de Propensity Score queda guardado en la variable W.hat. En cambio, el valor real de los datos queda guardado en la variable W.orig. Utilizaremos el creador de gráficos ggplot( ) de la librería ggplot2. Se construyen gráficos tipo histograma y tipo densidad de kernel.

ggplot(data.frame(W.hat = cf$W.hat, W = factor(cf$W.orig))) +
 geom_histogram(aes(x = W.hat, y = stat(density), fill = W), alpha=0.3, position = "identity") +
 geom_density(aes(x = W.hat, color = W)) +
 xlim(0,1) +
 labs(title = "Causal forest propensity scores",
      caption = "The propensity scores are learned via GRF's regression forest")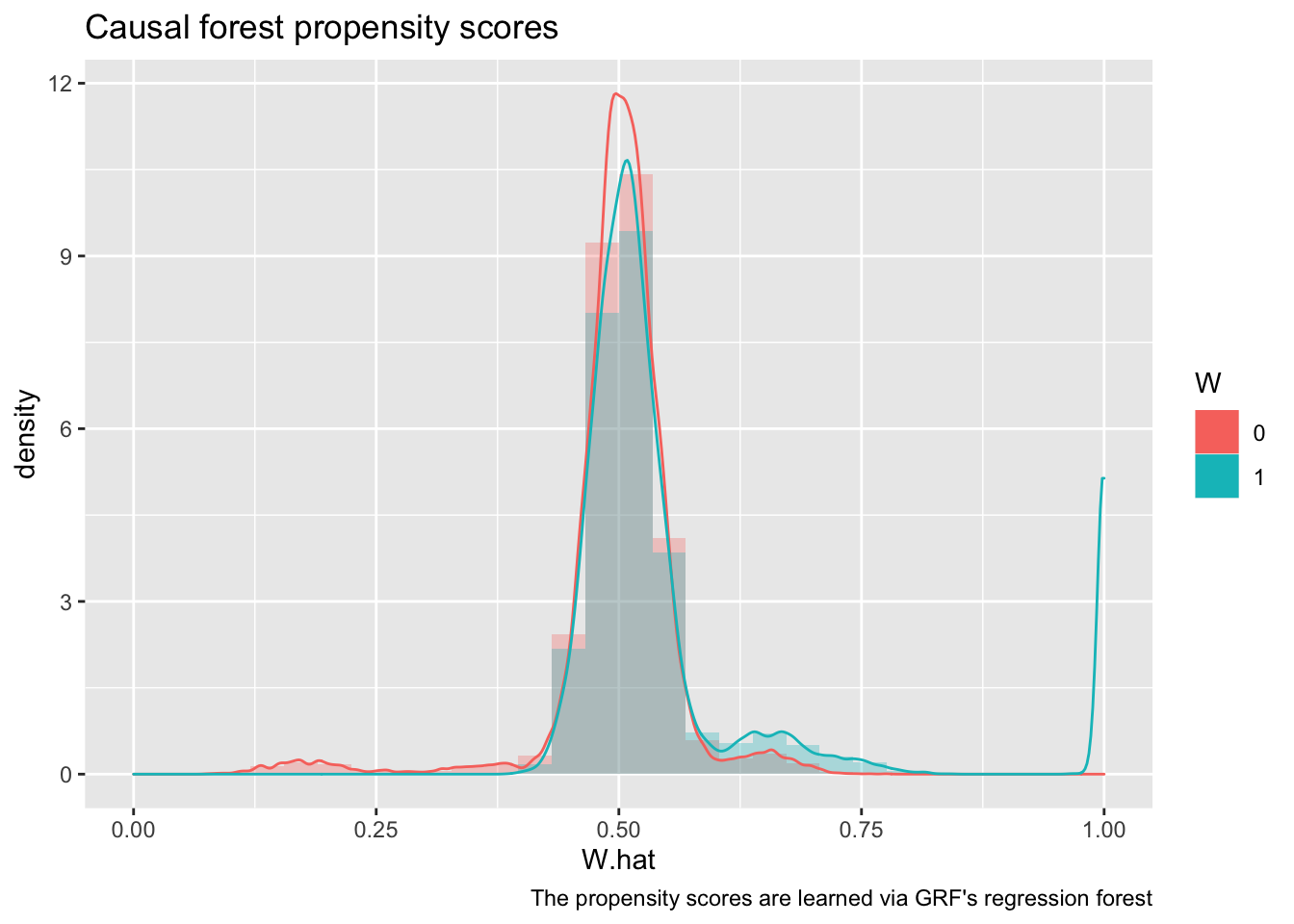

Estudiando el gráfico, ¿puede concluirse que existe región de soporte?

2.2 Estudiando la heterogeneidad

Utilizaremos la misma muestra de entrenamiento para estudiar la heterogeneidad de los efectos, por ello, utilizaremos errores “out of the bag” (OOB) para validar los resultados. Utilizaremos la función predict( ). Es también importante estimar los errores estándar de las predicciones, para examinar la significancia de ellas. Hay que recordar que las predicciones del \(CATE\) esperado se conocen como \(\hat{\tau}\), es decir, tau “gorro”, o tau “hat” en inglés.

oob_pred <- predict(cf, estimate.variance=TRUE)
oob_tauhat_cf <- oob_pred$predictions
oob_tauhat_cf_se <- sqrt(oob_pred$variance.estimates)

Para validar resultados utilizando el 20% de la muestra que quedó fuera, sólo se debe utilizar el parámetro newdata = en la función de predicción e incorporar allí la muestra de validación.

Se debe evaluar entonces si es que existe heterogeneidad de los efectos. Para ello graficamos un histograma de las estimaciones del CATE esperado (o tau hat).

hist(oob_tauhat_cf, main="Causal forests: out-of-bag CATE")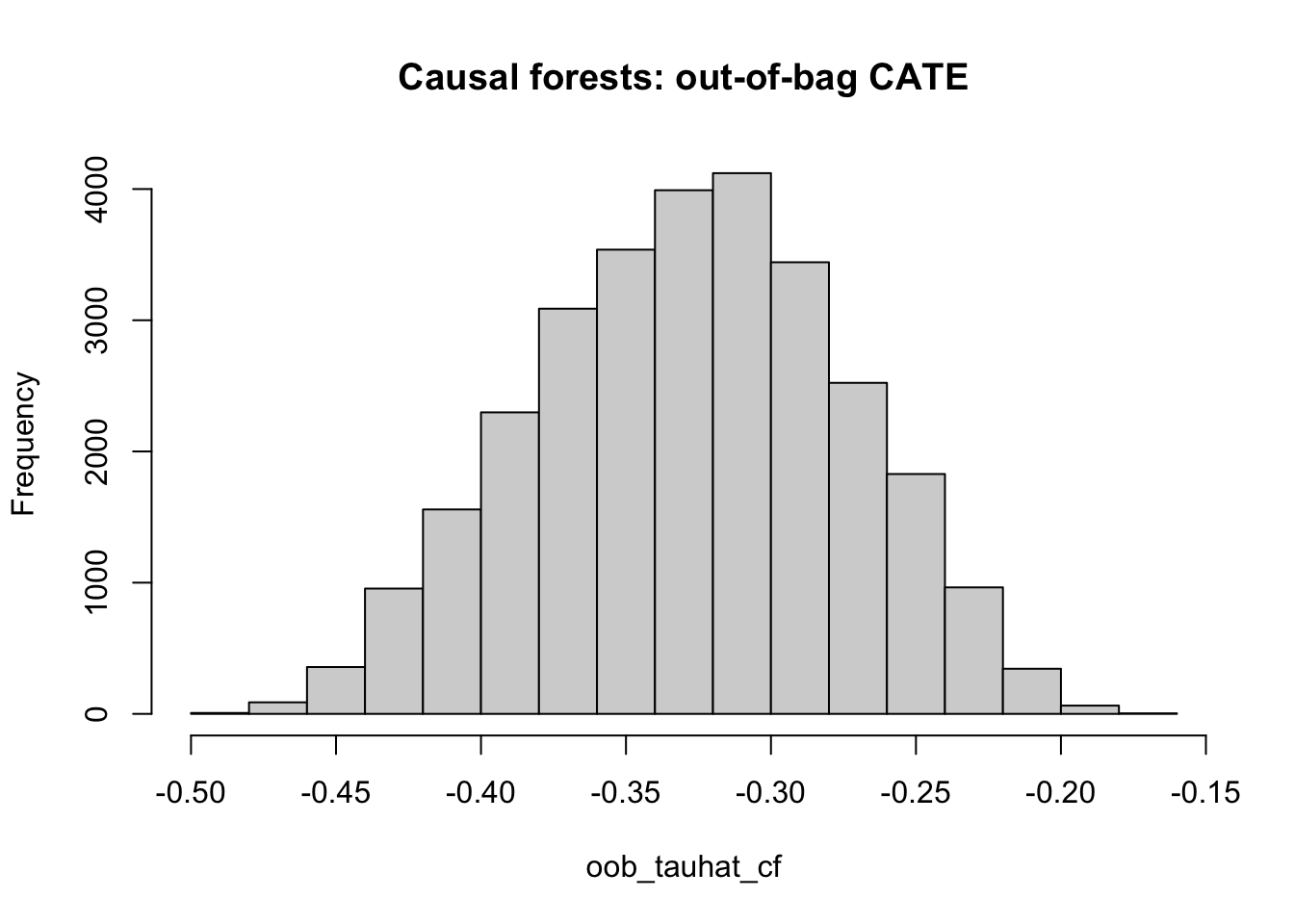

¿Existe heterogeneidad? ¿Se concentra en efectos positivos, negativos o ambos?

2.3 Importancia de Variables

La función utilizada permite estudiar cuáles fueron aquellas variables que más afectaron la construcción de los árboles. Al promediar cuánto aporta cada variable en disminuir la suma de errores cuadrados o la impureza de las hojas, entonces se puede “rankear” la importancia de las variables.

#Tabla
var_imp <- c(variable_importance(cf))
names(var_imp) <- colnames(as.data.frame(df_train %>% select(-c("Y", "W"))))
sorted_var_imp <- sort(var_imp, decreasing=TRUE)
head(sorted_var_imp, 15)

##         hrs1    hrs1_miss  evwork_miss       earnrs       speduc  sphrs1_miss 
##   0.10382318   0.05379900   0.05186639   0.05066754   0.04593565   0.04468485 
##          age         year         educ       evwork      spind80 wrkgovt_miss 
##   0.04236086   0.04171802   0.04102976   0.03682493   0.03662311   0.03376389 
##      widowed      wrkgovt     sppres80 
##   0.03056343   0.02665197   0.02402876

Es muy importante destacar que no sólo por estar abajo en el ranking de importancia quiere decir que una variable NO es importante para la heterogeneidad del efecto. Si dos variables tienen efectos importantes para la heterogeneidad, y tienen alta correlación entre ellas, puede ocurrir que el árbol utilice sólo una de ellas para la partición y no la otra, dejando a la primera alta en el ranking y a la segunda no.

\[\\[1in]\]

3. Heterogeneidad en subgrupos

Para esto, generaremos cuartiles del efecto de tratamiento. Ordenando la muestra desde la observación con menor \(CATE\) esperado hasta la observación con mayor CATE esperado, dividiremos la muestra en cuatro, generándose así cuatro cuartiles de observaciones, y que, por lo tanto, son grupos que permiten una comparación con un adecuado poder estadístico. Para la generación de cuartiles, y la incorporación de una columna a nuestra base de datos de entrenamiento utilizamos la función ntile( ). En este caso dividiremos la muestra en cuatro (cuartiles). Si dividiésemos la muestra en 5, serían quintiles.

num_tiles <- 4 
df_train$cate <- oob_tauhat_cf
df_train$ntile <- factor(ntile(oob_tauhat_cf, n=num_tiles))

Prueba cambiando el número de grupos de 4 a 5, y analiza cómo se modifican los resultados.

Para estimar el efecto de tratamiento (\(ATE\)) en cada subgrupo se pueden utilizar dos métodos. El primero compara “en bruto” las diferencias de resultado entre tratados y controles. El segundo método construye un estimador robusto. En escenarios experimentales ambos métodos debiesen llevar a resultados similares, pero en datos observacionales el segundo método asegura estimaciones insesgadas y eficientes.

3.1. Sample ATE

El primer método compara los efectos de tratamiento de tratados y de no tratados en cada uno de los cuartiles conformados. Para esto basta con realizar una regresión lineal (robusta), que nos permite a su vez estimar errores estandar. Esta regresión incluye términos de interacción con los indicadores de cada cuartil. La regresión con errores estándares robustos proviene de la función lm_robust, de la librería estimater.

#Para hacer la estimación
ols_sample_ate <- lm_robust(Y ~ ntile + ntile:W, data = df_train)

#Para que quede una tabla resumen con los resultados
estimated_sample_ate <- coef(summary(ols_sample_ate))[(num_tiles+1):(2*num_tiles), c("Estimate", "Std. Error")]

3.2. AIPW ATE

El segundo método es el \(Augmented\) \(Inverse-Propensity\) \(Weighted\) \(ATE\), o en español el \(ATE\) aumentado por ponderación de propensión inversa. Esto quiere decir que se ponderan las observaciones dentro de los cuartiles de acuerdo a (el inverso de) la probabilidad de haber sido tratados (Propensity Score). Esto debe hacerse por cada subgrupo.

ateq1 <-average_treatment_effect(cf,subset=df_train$ntile==1,method="AIPW")
ateq2 <-average_treatment_effect(cf,subset=df_train$ntile==2,method="AIPW")
ateq3 <-average_treatment_effect(cf,subset=df_train$ntile==3,method="AIPW")
ateq4 <-average_treatment_effect(cf,subset=df_train$ntile==4,method="AIPW")
estimated_aipw_ate <- data.frame(rbind(ateq1, ateq2, ateq3, ateq4))

Veamos cómo se comparan los resultados de ambos métodos en este escenario (experimental):

#Generando un data frame llamado G con columnas que indican el método y el cuartil de cada resultado:
  A <- as.data.frame(estimated_sample_ate)
  B <- as.data.frame(estimated_aipw_ate)
  colnames(A) <- c("Estimate", "Std. Error")
  colnames(B) <- c("Estimate", "Std. Error")
  G <- rbind(A,B)
  G$method <- c(1:8)
  G[1:4,]$method <- "Sample ATE"
  G[5:8,]$method <- "AIPW ATE"
  G$Cuartil <- c(1:8)
  G[c(1,5),]$Cuartil <- 1
  G[c(2,6),]$Cuartil <- 2
  G[c(3,7),]$Cuartil <- 3
  G[c(4,8),]$Cuartil <- 4
    
ggplot(G, aes(x=Cuartil, y=Estimate, colour=method)) +
      geom_point(position=position_dodge(.9)) +
      geom_errorbar(aes(ymin=Estimate-(1.647 * `Std. Error`),
                        ymax=Estimate+(1.647 * `Std. Error`), colour=method), 
                        width=.2,position=position_dodge(.9)) +
       theme(legend.title = element_blank(),panel.grid.major = element_blank()) +
       labs(x="Conditional Average Treatment Effect", #xlab() agrega etiqueta del eje X
       y="Frecuencia", #ylab() agrega etiqueta del eje y
       title="ATE en subgrupos" )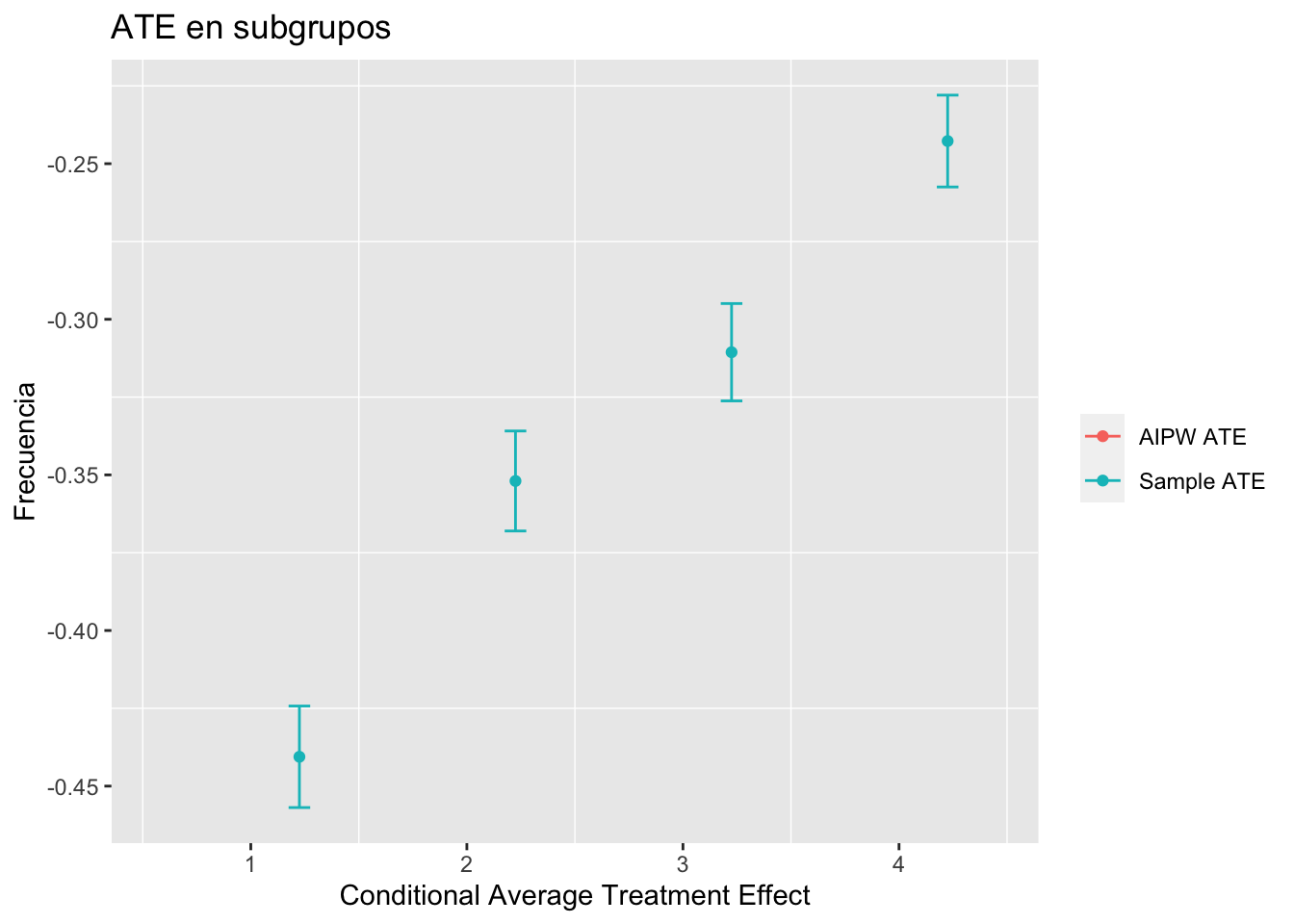

¿Se puede concluir que existen diferencias significativas en los \(ATE\) entre algunos grupos?

\[\\[1in]\]

4. BLP

Una forma de estudiar la variación del efecto de tratamiento es a través de la estimación del Best Linear Projection (o Best Linear Predictor). Este estudio permite, por un lado, evaluar la significancia de la heterogeneidad encontrada, a partir de un test motivado por Chernozhukov, Demirer, Duflo & Fernandez-Val (2018).

4.1 Test de calibración

El test consiste en utilizar un estimador que corrige la \(BLP\) de acuerdo a su Propensity Score y a los valores esperados. Para ver en detalle la forma del estimador, pueden dirigirse al artículo original de Chernozhukov et al. (2018), al Tutorial de Athey y colegas (2020), o al artículo de Murakami et al. (2020). Lo importante es tener en mente que se estima una regresión del estilo

\[Y_i - \hat{Y_i} = \alpha \cdot \hat{ATE} + \beta \cdot \hat{\tau_i}(x) + \varepsilon_i \]

donde las hipótesis nulas i) \(\alpha = 0\) indica que el valor del efecto de tratamiento para toda la muestra no es diferente de cero, y ii) \(\beta = 0\) no existe heterogeneidad en el efecto de tratamiento. De forma particular, en términos del ajuste del módelo, y siguiendo a Athey y colegas (2020), si es que \(\alpha = 1\) entonces la predicción promedio del ATE es adecuada, y si \(\beta = 1\) entonces las predicciones del Causal Forest capturan la heterogeneidad subyacente de forma adecuada.

tc <- test_calibration(cf)
tc

## 
## Best linear fit using forest predictions (on held-out data)
## as well as the mean forest prediction as regressors, along
## with one-sided heteroskedasticity-robust (HC3) SEs:
## 
##                                Estimate Std. Error t value    Pr(>t)    
## mean.forest.prediction         1.002122   0.014948  67.038 < 2.2e-16 ***
## differential.forest.prediction 1.403648   0.090092  15.580 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

4.2 Interpretaciones

Para estudiar el efecto de tratamiento con una covariable en particular, se puede utilizar la función best_linear_projection( ) para ver la magnitud de las pendientes. En este caso comenzaremos con la variable que indica si el sujeto en estudio está divorciado o no. ¿Cómo se interpreta este resultado?

best_linear_projection(cf, df_train$divorce)

## 
## Best linear projection of the conditional average treatment effect.
## Confidence intervals are cluster- and heteroskedasticity-robust (HC3):
## 
##              Estimate Std. Error  t value  Pr(>|t|)    
## (Intercept) -0.434460   0.031484 -13.7994 < 2.2e-16 ***
## A1           0.073087   0.019361   3.7749 0.0001607 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Prueba con otras covariables, puedes comenzar por aquellas que están en los primeros lugares del ranking de importancia.

4.3 Optimización

Entendiendo que las Best Linear Projection permite estudiar que el efecto de tratamiento varía con una determinada covariable: ¿cómo se interpretaría la heterogeneidad del efecto estudiado en este caso para las variables que escogiste? Este estudio de caso no es una programa o política pública determinada, sino que es un tratamiento experimental para evaluar las percepciones sobre las políticas de bienestar.

En cambio, si estuviéramos estudiando una política o programa, sería de interés poder diseñar un óptimo.

Chernozhukov, V., Demirer, M., Duflo, E., & Fernandez-Val, I. (2018). Generic Machine Learning Inference on Heterogeneous Treatment Effects in Randomized Experiments, with an Application to Immunization in India (No. w24678). National Bureau of Economic Research.

Murakami, K., Shimada, H., Ushifusa, Y., & Ida, T. (2020). Heterogeneous Treatment Effects of Nudge and Rebate: Causal Machine Learning in a Field Experiment on Electricity Conservation (No. e-20-003).

Para profundizar los contenidos y aplicaciones presentados en este tutorial, te invitamos a revisar de manera opcional el siguiente enlace, que es un Data Tutorial -en inglés- diseñado por Susan Athey.